Ongoing activities

Impact in a granular medium
Collaborators : D. Carvalho, J. Crassous, B. Darbois Texier, E. Franklin, P. Gondret, A. Seguin
The impact of a projectile into a granular medium involves two primary mechanisms: inertial resistance, arising from grain collisions, and a depth-dependent force, analogous to hydrostatic pressure in a fluid [9].
The penetration depth follows a robust scaling law that depends primarily on the projectile’s density and the impact energy (drop height).
When either the medium or the projectile is set into rotation, penetration increases significantly (by up to 15%), due to localized fluidization of the grains, which reduces friction [21].
Lateral walls also play a critical role: even moderate confinement (container-to-projectile diameter ratio below 5) drastically reduces penetration [8].
In the specific case of pile driving by successive impacts (repetitive percussion), the dynamics transition from a linear regime to progressive deceleration, with the final penetration depth decreasing as confinement becomes more pronounced.
Lateral walls, by restricting the medium’s dilatancy, can even halt penetration entirely [18].
These mechanisms shed light on phenomena ranging from impact crater physics to the design of drilling tools.
They also open avenues for applications in civil engineering (foundations, soil stabilization), ballistic protection (granular shields), and space exploration (burrowing robots, planetary probes).

Controlling avalanches with barriers
Collaborators : J. Benito, B. Darbois Texier, I. Ippolito, P. Gondret
Granular flows on inclined planes, such as avalanches or landslides, can be effectively controlled using networks of obstacles. Our experiments demonstrate that these obstacles significantly enhance the stability of granular layers by increasing the critical avalanche angle [11] and reducing steady-state flow rates [19]. This effect arises from additional friction induced by the obstacles, which scales with their density and the thickness of the granular layer. The results reveal that obstacles profoundly alter flow dynamics: without obstacles, the flow rate grows superlinearly with grain thickness, but their presence mitigates this dependence, leading to saturation in the densest configurations and nearly eliminating sensitivity to thickness. A model combining the µ(I) rheology and an additional drag force successfully predicts these behaviors, confirming the existence of a threshold obstacle density beyond which their stabilizing effect becomes significant. This work offers practical insights for natural hazard mitigation (e.g., slope stabilization using forests or artificial structures) and industrial optimization (e.g., controlling flows in silos or conveyors).

Title
Collaborators :
Description.
Past activities

The amazing properties of egg white revealed by its microstructure
Collaborators : B. Darbois Texier, L. Pauchard
Egg white, a common household fluid, exhibits complex rheology: its network of entangled proteins imparts both viscoelasticity and shear-thinning behavior, where viscosity decreases under stress [17]. This property facilitates air incorporation during whipping, while its elastic shear modulus (~2.3 Pa) and low-shear viscosity (0.2–0.4 Pa·s) reflect its ability to stabilize the resulting structure. Viscosity also plays a key role in the spinning egg test: when a raw egg is briefly stopped, its fluid interior continues moving, causing the shell to resume rotation. This dynamic is described by a simple model based on the diffusion of the no-slip boundary condition, which reproduces the decay of residual velocity and provides a viscosity estimate (~0.23 Pa·s) consistent with rheological measurements. Additionally, drying an egg white film produces anisotropic cracks aligned with the spreading direction, a signature of protein orientation. These findings illustrate how protein microstructure governs macroscopic behaviors, from foam stabilization to the design of bio-inspired materials.

Competition between two erosion patterns at the base of a cylinder
Collaborators : P. Gondret, F. Lachaussée, C. Morize, A. Sauret
The erosion of a granular bed around a vertical cylinder—a well-documented phenomenon in hydraulics and geomorphology—is typically dominated by horseshoe scouring at the base of the obstacle. This pattern, caused by the contraction of streamlines and an enveloping vortex, emerges once the Shields number (the ratio of shear stress to grain weight) exceeds a critical threshold. It prevails under intense flow conditions, reaching depths of up to 40% of the cylinder’s diameter. The novelty of this study lies in identifying a previously overlooked second erosion pattern: two symmetrical elongated scour holes forming downstream of the cylinder due to the alternating Bénard-von Kármán vortices [14]. Though shallower, this pattern is more extensive and develops under flow conditions near the threshold for horseshoe scouring. However, it is quickly suppressed by the latter as flow intensity increases, revealing a dynamic competition between the two processes. These observations—where the onset thresholds depend only weakly on the cylinder’s diameter—offer insights for fine-scale modeling of scour around structures (e.g., bridge piers, offshore foundations) and for understanding geomorphological patterns downstream of obstacles. They also highlight the importance of considering interactions between erosion patterns to predict the evolution of granular beds under turbulent flows.
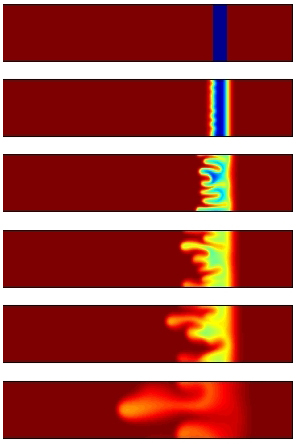
Viscous fingering of miscible fluids
Collaborators : A. De Wit, M. Martin
Viscous fingering is an instability that occurs when a less viscous fluid displaces a more viscous fluid in a porous medium. Here, we focus on the case of miscible fluids [6], which contrasts with many prior studies conducted on immiscible fluids. We demonstrate that, in a finite-width slice, fingering is transient because progressive dilution reduces the viscosity contrast driving the instability. Using numerical simulations based on Darcy’s law and solute concentration evolution, we investigate the key parameters influencing viscous fingering dynamics. The mobility ratio (comparing the viscosity of the displaced fluid to that of the injected fluid) significantly amplifies instability when high. Similarly, the Péclet number (the ratio of advection to diffusion) intensifies the phenomenon at high flow rates or in large-scale systems. Additionally, the ratio of transverse to axial dispersion plays a stabilizing role: the more isotropic the diffusion, the more the fingering is suppressed. This understanding is critical for interpreting peak broadening in chromatography, pollutant propagation in aquifers, and other scenarios where miscible fluids of differing viscosities interact, such as saline solution transport in aquifers or certain chemical and pharmaceutical processes in porous media.
